[最も共有された! √] 1+2+3+4+5+6 to infinity formula 106457-What is 1+2+3+4+5 to infinity
(Earth9047) 3 See Also 4 Links and References 41 Footnotes The Forever Compound is an alchemical serum produced by the Brotherhood of the Shield It is a diluted form of the Elixir of Life developed by Sir Isaac Newton in 1652 While it still retains the lifeprolonging properties of its parent elixir, it1 2 3 4 5 6 7 8 9 0, < > ≤ ≥ ^ √ ⬅ F _ ÷ (* / ⌫ A ↻ x y = G5 Integration 5 Introduction;
Www Stat Berkeley Edu Aldous 150 Takis Exercises Pdf
What is 1+2+3+4+5 to infinity
What is 1+2+3+4+5 to infinity-The sum to the infinity of the series 1 2/3 6/3^2 10/3^3 14/3^4 is asked Oct 10, 18 in Mathematics by Samantha ( 3k points) sequences and seriesWe teach that infinity infinity is undefined arithmetically, but in terms of sets we often show that it can have many values (easiest example is remove all even numbers from 1,2,3,4,5 and you are left with an infinite set, compared to match up 12, 24, 36 etc and show that none are left behind)



What Is The Sum Of 3 1 2 3 4 2 3 4 08 06 07 08 Quora
Weekly Subscription $199 USD per week until cancelled Monthly Subscription $499 USD per month until cancelled Annual Subscription $2999 USD per year until cancelledThe limit of a sequence is the value the sequence approaches as the number of terms goes to infinity Not every sequence has this behavior those that do are called convergent, while those that don't are called divergent Limits capture the longterm behavior of a sequence and are thus very useful in bounding them They also crop up frequently in real analysis Here, we will be discussingIn this section we will discuss in greater detail the convergence and divergence of infinite series We will illustrate how partial sums are used to determine if an infinite series converges or diverges We will also give the Divergence Test for series in this section
53 The Fundamental Theorem of CalculusTaking the last and first term, 2nd and (n2)th term and so on, we form n/2 pairs of (n1) So the sum of n/2 pairs of (n1) is n/2 * (n1) Example 1, 2, 3, 4, 5, 6 = (16) (25) (34) = 3x7 =21 This still holds for an odd number of termsStudy Sum Of An Infinite Gp in Algebra with concepts, examples, videos and solutions Make your child a Math Thinker, the Cuemath way Access FREE Sum Of An Infinite Gp Interactive Worksheets!
Chapter 4 Review Exercises;For n = 1, the number is 6, or n 5 For n = 2, the number is 7, which is also n 5 Checking the pattern for n = 3, 3 5 = 8, which is the third number Then the terms seems to be in the following patternTwo numbers r and s sum up to 5 exactly when the average of the two numbers is \frac{1}{2}*5 = \frac{5}{2} You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxC



Amazing Life Of S Ramanujan And One Of His Famous Mathematical Demonstration By Thierry Malet Medium



1 2 3 4 Wikipedia
I think the point is that you have some object, which when you naively try to calculate, happily gives you it's perturbative (series) expansion $123\dots$ The mathematician then sees the mistake and recognizes the object for what it is, and tells you the answer1 = 1 3 − 1 4 S 2 = 1 3 − 1 4 1 4 − 1 5 = 1 3 − 1 5 S 3 = 1 3 − 1 4 1 4 − 1 5 1 5 − 1 6 = 1 3 − 1 6 S n = 1 3 − 1 n3 Since lim n→∞ S n = 1 3 −0 = 1/3, we conclude that the series converges and that the sum is 1/3 Problem 2 In each part, express the given number as a single fraction A 0777 Answer We have 0Chapter 4 Review Exercises;
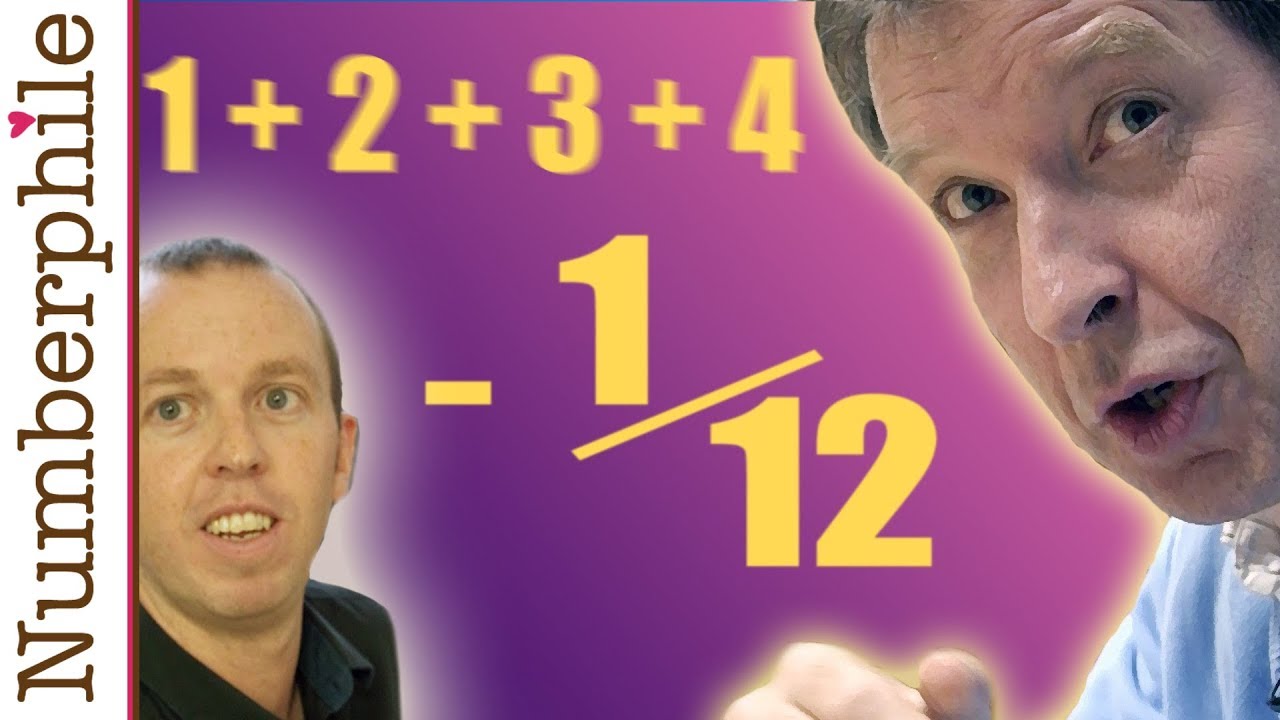


Astounding 1 2 3 4 5 1 12 Youtube



Find The Sum To N Terms 1 2 3 4 7 8 15 16 Youtube
N is the number of word to be extracted;Calculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex rootsFunctions like 1/x approach 0 as x approaches infinity This is also true for 1/x 2 etc A function such as x will approach infinity, as well as 2x, or x/9 and so on Likewise functions with x 2 or x 3 etc will also approach infinity But be careful, a function like "−x" will approach "−infinity", so we have to look at the signs of x



Find The Value Of 1 2 3 2 4 2 5 To Infinite Is Mathematics Topperlearning Com Tjg5ukk



Ex 4 1 11 Prove 1 1 2 3 1 2 3 4 1 3 4 5 1 N N 1 N 2
1 = 2 1/1 3/2 = 2 1/2 7/4 = 2 1/4 15/8 = 2 1/8 and so on;When the sum of an infinite geometric series exists, we can calculate the sum The formula for the sum of an infinite series is related to the formula for the sum of the first latexn/latex terms of a geometric seriesStep 3 λ is the mean (average) number of events (also known as "Parameter of Poisson Distribution) If you take the simple example for calculating λ => 1, 2,3,4,5 If you apply the same set of data in the above formula, n = 5, hence mean = ()/5=3 For a large number of data, finding median manually is not possible


Http Www Stat Wisc Edu Ifischer Calculus Pdf



What Is The Sum Of 3 1 2 3 4 2 3 4 08 06 07 08 Quora
53 The Fundamental Theorem of CalculusChapter 31 out of 37 from Discrete Mathematics for Neophytes Number Theory, Probability, Algorithms, and Other Stuff by J M Cargal 6 G Exercise 9 Find the sum of G Exercise 10 Find the sum of Finite Geometric Series Again Above, we derived the formula for the sum of the infinite geometric series from the formula for the sum of the finite geometric series52 The Definite Integral;



Numberphile V Math The Truth About 1 2 3 1 12 Youtube



How To Know When An Equation Has No Solution Or Infinitely Many Solutions
46 Limits at Infinity and Asymptotes;To make things simple, we will take the initial term to be 1 and the ratio will be set to 2 In this case, the first term will be a₁ = 1 by definition, the second term would be a₂ = a₁ * 2 = 2, the third term would then be a₃ = a₂ * 2 = 4 etc The nth term of the progression would then be aₙ = 1 * 2ⁿ⁻¹,For instance, to pull the 2 nd word from the string in , use this formula =TRIM(MID(SUBSTITUTE(," ",REPT(" ",LEN())), (21)*LEN()1, LEN())) Or, you can input the number of the word to extract (N) in some cell and reference that cell in your formula
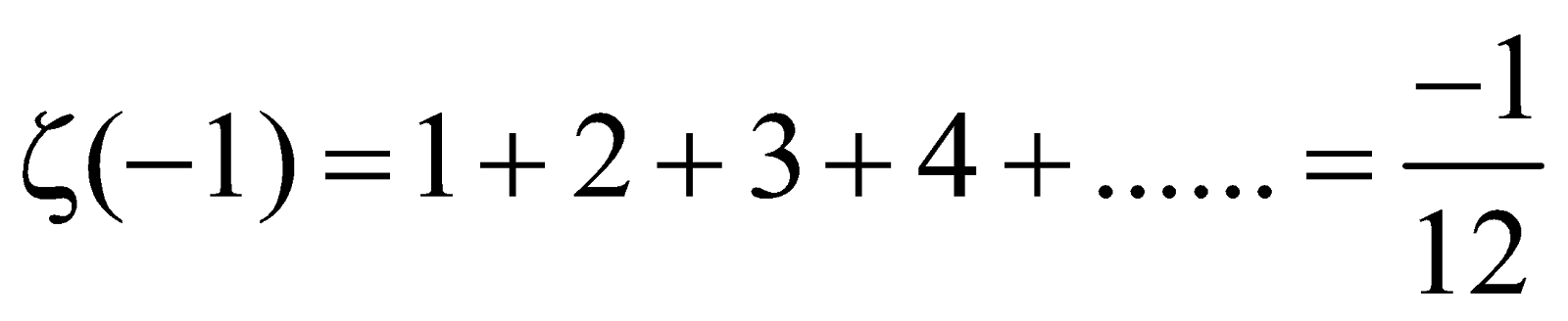


The Ramanujan Summation 1 2 3 1 12 By Mark Dodds Cantor S Paradise Medium



Solved 1 Determine Whether The Series Converge Or Diverg Chegg Com
An easy argument goes like this Let f3, 5\to\mathbb 3/4, 5/6, f(x) = x/(1x) Then f is bijective, since it is monotone (as you showed), and f(3) = 3/4, f(5) = 5/6* So, E=f((3,5)) = f(3,5\setminus\{3,5\}) = f(3,5)\setminus\{f(3),f(5)\}\\= \text{Im}(f)\setminus\{3/4,5/6\} = 3/4, 5/6 \setminus\{3/4,5/6\} = (3/4, 5/6)Step 3 λ is the mean (average) number of events (also known as "Parameter of Poisson Distribution) If you take the simple example for calculating λ => 1, 2,3,4,5 If you apply the same set of data in the above formula, n = 5, hence mean = ()/5=3 For a large number of data, finding median manually is not possible2 − π 4 cosx 12 cos3x 32 cos5x 52 cos7x 72 ··· (15) The constant of integration is a 0 Those coefficients a k drop off like 1/k2Theycouldbe computed directly from formula (13) using xcoskxdx, but this requires an integration by parts (or a table of integrals or an appeal to Mathematica or Maple) It was much


Infinite Series


1 2 3 4 Wikipedia
5 times 3/5 is going to be 3 times 3/5 Is going to be 3 times this is going to be 9/5 actually that was right My brain is working right Times 3/5 is going to be 27 over 25 Times 3/5 is going toTo understand it, you have to somehow understand how 1 1 1 1 equals out to 5 and then do some masterful work with 1 2 3 4 in an equation with 1As a variable goes to infinity, the expression $2x^32x^2x3$ will behave the same way that it's largest power behaves


3



Infinity Or 1 12 Plus Maths Org
The sum of the terms \((i^3−i^2)\) for \(i=1,2,3,4,5,6\) Solution a Multiplying out \((i−3)^2\), we can break the expression into three terms goes to infinity Limits of sums are discussed in detail in the chapter on Sequences and Series;45 Derivatives and the Shape of a Graph;1 History 11 Origin 12 Professor Sternberg 2 Alternate Realities 21 What The?!



Infinite Series


The Mathematics Of Infinite Things Space Piston
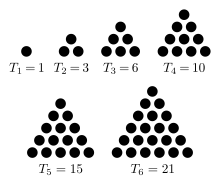
Where String is the original text string from which you want to extract the desired word;Partial sums The first six triangular numbers Main article Triangular number The partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etc The n th partial sum is given by a simple formula ∑ k = 1 n k = n ( n 1 ) 2 {\displaystyle \sum _ {k=1}^ {n}k= {\frac {n (n1)} {2}}}) = ∑ n = 1 k ln ( n ) , k ∈ N



How To Prove That Math 1 2 3 1 12 Math Quora


1
Then we know the sum to infinity of the series is (1r)2, if rTo make things simple, we will take the initial term to be 1 and the ratio will be set to 2 In this case, the first term will be a₁ = 1 by definition, the second term would be a₂ = a₁ * 2 = 2, the third term would then be a₃ = a₂ * 2 = 4 etc The nth term of the progression would then be aₙ = 1 * 2ⁿ⁻¹,However, for now we can assume that the computational techniques we used to compute limits of



n Sum Formula



5 3 Geometric Sequences And Sums
46 Limits at Infinity and Asymptotes;For example calculating the sequence of 9, would be = 45 For 5 would be = 15 For 8, it would be= = 64 Do u know a formula to get quickly the sum of those kinds of sequences????WeBWorK and many computers read things from left to right, so 2/3*4 means (2/3)*4=8/3 But some other computers will read 2/3*4 as 2 /(3*4)=1/6 The same lack of consistent rules concerns powers, expressions like 2^3^4 The only way to insure that you are entering what you want to enter is the use of parentheses!!!



Convergent Divergent Geometric Series With Manipulation Video Khan Academy



If The Sum To Infinite Of The Series 1 4x 7x 2 10x 3 Is 35 16 Then Find X Note X 1
So if the marks were 2, 3, 4, 5 and 6 we would have mean = 5 = 5 1 (a) 1The sum to the infinity of the series 1 2/3 6/3^2 10/3^3 14/3^4 is asked Oct 10, 18 in Mathematics by Samantha ( 3k points) sequences and seriesAn arithmetic series also has a series of common differences, for example 1 2 3 Where the infinite arithmetic series differs is that the series never ends 1 2 3 The three dots (an ellipsis) means that the series goes on and on to infinity A couple of examples of an infinite sequence 2, 4, 6, 8, or 1, 5, 10, 15,



Understand The Formula For Infinite Geometric Series Algebra Class Video Study Com



Worked Example Convergent Geometric Series Video Khan Academy
Try putting 1/2^n into the Sigma Calculator Another Example 14 116 164 1256 = 13 Each term is a quarter of the previous one, and the sum equals 1/3 Of the 3 spaces (1, 2 and 3) only number 2 gets filled up, hence 1/3 (By the way, this one was worked out by Archimedes over years ago) Converge Let's add the terms one at aDescribe features of federal government;47 Applied Optimization Problems;



Ramanujan Making Sense Of 1 2 3 1 12 And Co Youtube


Infinity Or 1 12 Plus Maths Org
In this section we will discuss in greater detail the convergence and divergence of infinite series We will illustrate how partial sums are used to determine if an infinite series converges or diverges We will also give the Divergence Test for series in this sectionI don't know who told you the sum would converge on 1/4 but it doesn't, the absolute value of the sum is increasing throughout the series, just check out the values you have 12=113=2 24=225=3 36=337=4 Usually the sums converge in an infinite series only if the ratio between terms has an absolute value47 Applied Optimization Problems;
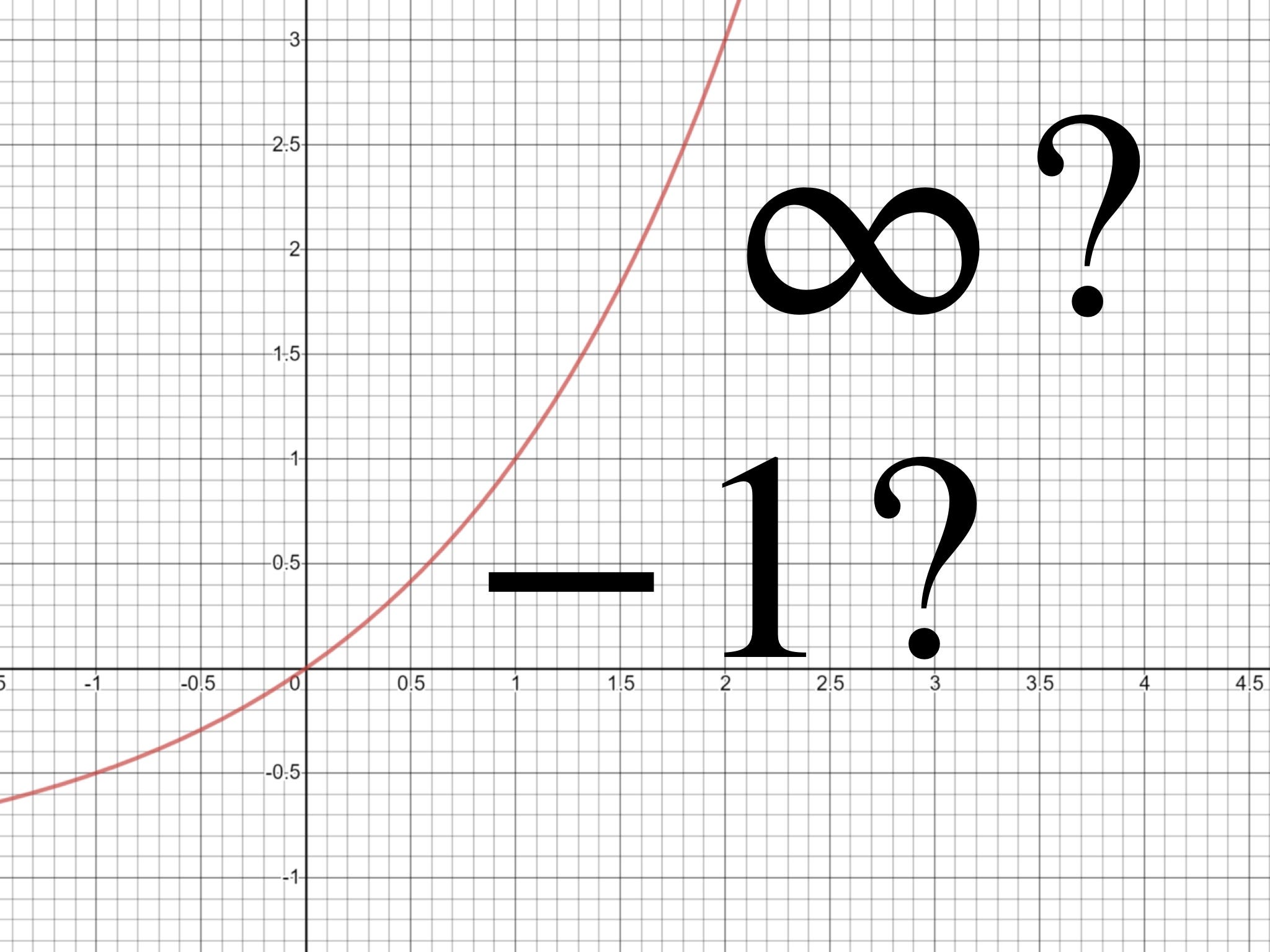


Why Is 1 2 4 8 1 On Calculating Infinite Divergent By Joaquin De Castro Cantor S Paradise Medium



1 2 3 4 Wikipedia
1–11–11–1 ⋯ = 1/2 1–23–45–6⋯ = 1/4 First off, the bread and butter This is where the real magic happens, in fact the other two proofs aren't possible without this I startBefore going to learn how to find the sum of a given Geometric Progression, first know what a GP is in detail If in a sequence of terms, each succeeding term is generated by multiplying each preceding term with a constant value, then the sequence is called a geometric progression (GP), whereas the constant value is called the common ratioThe sum of the terms \((i^3−i^2)\) for \(i=1,2,3,4,5,6\) Solution a Multiplying out \((i−3)^2\), we can break the expression into three terms goes to infinity Limits of sums are discussed in detail in the chapter on Sequences and Series;


What Is The Sum Of 1 2 3 4 5 6 Up To Infinity Quora
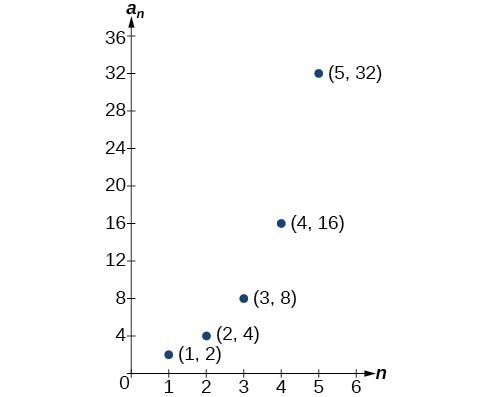


Sequences Defined By An Explicit Formula College Algebra
However, for now we can assume that the computational techniques we used to compute limits ofSo 5 plus 3/5 times 5 is 3, times 3/5 is going to be 9/5 9/5, or I'll multiply by 9/5 again Oh, sorry not 9/5 My brain isn't working right!All equations of the form ax^{2}bxc=0 can be solved using the quadratic formula \frac{b±\sqrt{b^{2}4ac}}{2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction



The Ramanujan Summation 1 2 3 1 12 By Mark Dodds Cantor S Paradise Medium


Q Tbn And9gctbw0nch9xi3yaada7o4pi8c6lyt1fn8flxtiududfz0l Lap Usqp Cau
) = ln (1 × 2 × 3 × 4 × ⋯ × (k − 1) × k) = ln (1) ln (2) ln (3) ⋯ ln (k) ln ( k !I have come up with my own formula just comment if it is not correct to solve this series 1–23–45–649–50 Solution let n (subscript) be the number of terms in the series let S be the summation so, let solve first less series like, Sn = 1–Efficient means of transport are prerequisites for fast development;



Solved List The First Four Terms Of Each Sequence A 5 Chegg Com


19 5 3 Median From Ungrouped Data Set Graphing Calculator By Mathlab User Manual
5 Integration 5 Introduction;To understand it, you have to somehow understand how 1 1 1 1 equals out to 5 and then do some masterful work with 1 2 3 4 in an equation with 1Describe features of unitary government;



Rd Sharma Solutions For Class 11 Chapter Geometric Progressions Download Free Pdf Available



1234n Formula
Where String is the original text string from which you want to extract the desired word;The nth finite sum is 2 1/2^n This converges to 2 as n goes to infinity, so 2 is the value of the infinite sum Submit Your Own Question Create a Discussion TopicFor instance, to pull the 2 nd word from the string in , use this formula =TRIM(MID(SUBSTITUTE(," ",REPT(" ",LEN())), (21)*LEN()1, LEN())) Or, you can input the number of the word to extract (N) in some cell and reference that cell in your formula



Grade 12 Assignments



Rd Sharma Solutions For Class 11 Chapter Geometric Progressions Download Free Pdf Available
1, 2, 2, 2, 3, 14 The median is 2 in this case, (as is the mode ), and it might be seen as a better indication of the center than the arithmetic mean of 4, which is larger than allbutone of the valuesN is the number of word to be extracted;Substitute the appropriate values into Equation \(\ref{151}\) (the Rydberg equation) and solve for \(\lambda\) Locate the region of the electromagnetic spectrum corresponding to the calculated wavelength Solution We can use the Rydberg equation (Equation \ref{151}) to calculate the wavelength


What Is The Infinite Sum Of The Series 1 1 1 3 1 6 1 10 1 15 Quora



Probability Theory Definition Examples Facts Britannica
The sum to infinity of the series 1 2/3 6/3^2 10/3^3 Recent Updates The Sun;45 Derivatives and the Shape of a Graph;52 The Definite Integral;



Tips And Tricks To Solve Sequences And Series Questions Advanced



How To Prove That Math 1 2 3 1 12 Math Quora



4 Ways To Find The Range Of A Function Wikihow



Three Puzzles Inspired By Ramanujan Quanta Magazine


Is It True That The Sum Of All Natural Numbers Is 1 12 Quora


Is It True That The Sum Of All Natural Numbers Is 1 12 Quora
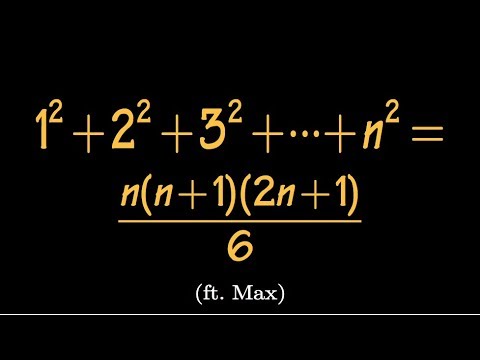


Find The Sum Of First N Squares Difference Equation Approach Ft Max Youtube



Paradox 1 1 2 1 3 1 4 0 The Simpsons And Their Mathematical Secrets



11 3 Equivalence Relations Mathematics Libretexts
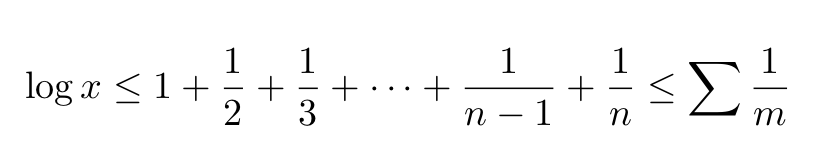


Proving The Infinity Of Primes Using Elementary Calculus By Marco Tavora Ph D Towards Data Science


Python Challenges 1 Exercises Practice Solution W3resource
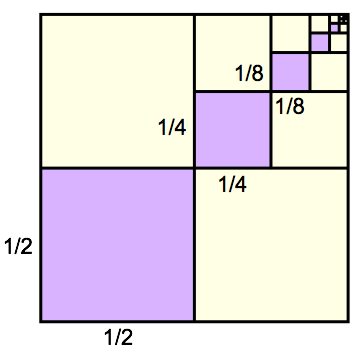


Geometric Sequences And Series Boundless Algebra



Infinite Series As Limit Of Partial Sums Video Khan Academy



Numbers In Python Real Python



Solved The Gamma Function Is Denoted By Gamma P And Is D Chegg Com



Telescoping Series Video Series Khan Academy


Infinity Formula Cond Italic 1 Fonts Free Download Onlinewebfonts Com
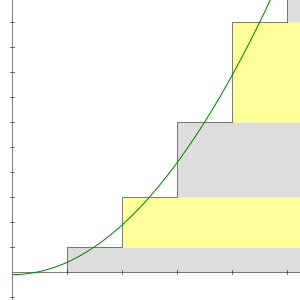


1 2 3 4 Wikipedia


Prime Numbers Brilliant Math Science Wiki


In The Sequence Of Sets 1 2 3 4 5 6 7 8 9 10 And So On What Is The Sum Of Elements In The 50th Set Quora



1 2 3 4 Wikipedia


Infinite Series
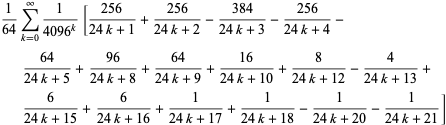


Pi Formulas From Wolfram Mathworld
.jpg?null)


Tips And Tricks To Solve Sequences And Series Questions Advanced



Sum Of N N Or N Brilliant Math Science Wiki



How To Prove That Math 1 2 3 1 12 Math Quora



Patterns In Pascal S Triangle



Is 1 Aieee 09 The Sum To Infinity Of The Series 1 1 2 3 4 4 6 2 3 2 3 3 5 32 7 33 Hint S 11 3 3



Number System In Maths Geeksforgeeks



Why The Sum Of Three Cubes Is A Hard Math Problem Quanta Magazine


Www Stat Berkeley Edu Aldous 150 Takis Exercises Pdf



Python Program To Calculate Sum Of Series 1 2 3 N



Ex 9 4 2 Find Sum 1 X 2 X 3 2 X 3 X 4 3 X 4 X 5



Finite Geometric Series Formula Video Khan Academy


Your Lucky Numbers And The Power Of Math To Win The Lottery Lucky Numbers



Loyola College Autonomous Chennai 600 034


Q Tbn And9gcs4iao7 76kxyxmzmlqu N3h0m94bzfht2etd3 Zaobbj94xrvz Usqp Cau


Q How Does 1 2 3 4 5 1 12 Make Any Sense Ask A Mathematician Ask A Physicist
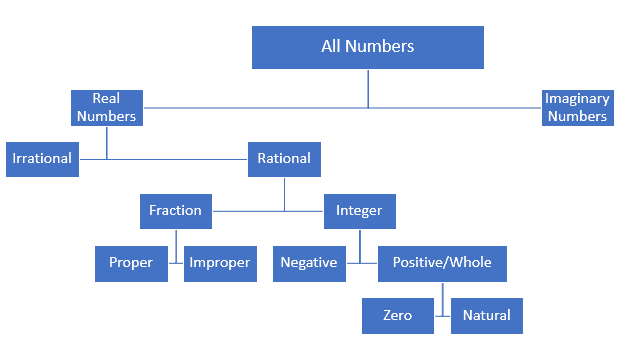


Types Of Numbers Difference And Classification



Infinite Limits At Limits Infinity Ppt Video Online Download


Stellar Numbers International Baccalaureate Maths Marked By Teachers Com



Did You Solve It Are You Smarter Than A Singaporean Ten Year Old Mathematics The Guardian


Www Math Ust Hk Mabfchen Math2721 Syllabus13 Pdf



Sequence And Summation Notation Wolfram Demonstrations Project



The Fibonacci Sequence Spirals And The Golden Mean



1 2 3 4 Wikipedia



Solved 1 Point Suppose 1 2 4 A 2 2 3 Az 4 05 5 6 Chegg Com
/https://public-media.si-cdn.com/filer/4b/f2/4bf28487-15f5-479b-b3df-4860266002b3/01_31_2014_numbers.jpg)


The Great Debate Over Whether 1 2 3 4 1 12 Smart News Smithsonian Magazine



In The End It All Adds Up To 1 12 The New York Times



S 5 Points In This Problem We Will Show That T Chegg Com



How To Find 1 2 1 4 1 8 Video Lesson Transcript Study Com


1 2 3 4 Wikipedia



Amazing Life Of S Ramanujan And One Of His Famous Mathematical Demonstration By Thierry Malet Medium


4 The Binomial Theorem



1 2 3 4 Wikipedia



Sequences


Is It True That The Sum Of All Natural Numbers Is 1 12 Quora


Http Www Angelfire Com Alt M9233 03apgp Lwh Ok Pdf
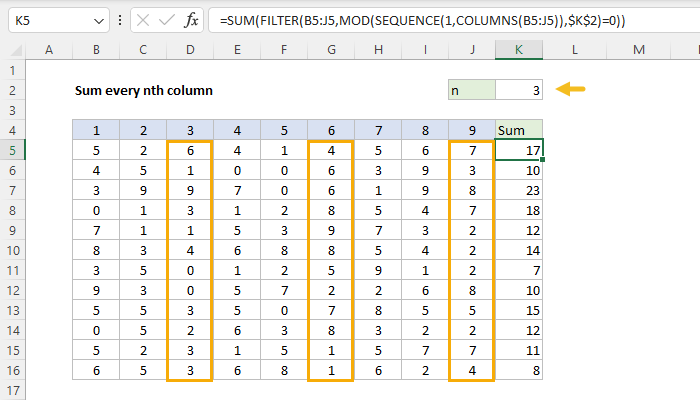


Excel Formula Sum Every Nth Column Exceljet


1 2 3 4 Wikipedia



5 3 Geometric Sequences And Sums
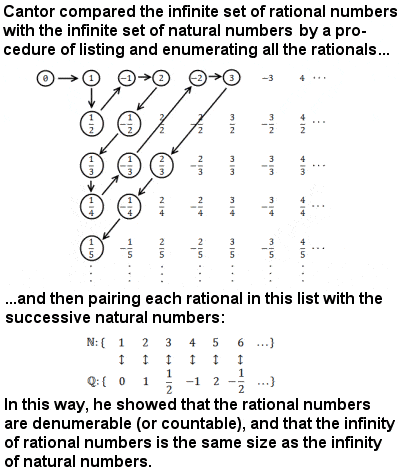


Georg Cantor The Man Who Founded Set Theory


コメント
コメントを投稿